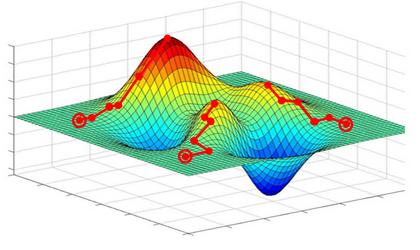
Optimisation methods used in computational modelling

2023, Jun 23    

Optimisation methods used in computational modelling

1. Local optimisation

Nelder Mead algorithm It is a numerical method using simplex, not a true global optimisation method. A simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example, a 0-dimensional simplex is a point, a 1-dimensional simplex is a line segment, a 2-dimensional simplex is a triangle, a 3-dimensional simplex is a tetrahedron, and a 4-dimensional simplex is a 5-cell.

Nelder-Mead is a popular optimization algorithm used for minimizing a given objective function. While it is commonly used for unconstrained optimization, it can also be adapted for the minimization of error using residuals in the context of nonlinear regression or curve fitting problems.

In order to minimize error using residuals with the Nelder-Mead algorithm, you would typically follow these steps:

1. Define your objective function: In the context of curve fitting or regression, the objective function is typically the sum of squared residuals. Residuals represent the differences between the observed data points and the values predicted by your model.

2. Initialize the simplex: The Nelder-Mead algorithm operates on a simplex, which is a set of points in the parameter space. The initial simplex is typically constructed around an initial guess for the parameter values.

3. Evaluate the objective function: Compute the sum of squared residuals for each point in the simplex. This involves fitting the model to the data using the current parameter values and calculating the residuals.

4. Update the simplex: Based on the evaluations of the objective function, the Nelder-Mead algorithm updates the simplex by performing a set of operations such as reflection, expansion, contraction, and shrinkage. These operations move the simplex towards the optimal solution.

5. Repeat steps 3 and 4: Evaluate the objective function for the updated simplex and continue updating the simplex iteratively until a stopping criterion is met. The stopping criterion can be a maximum number of iterations, reaching a desired error threshold, or other conditions specific to your problem.

6. Retrieve the optimal parameter values: Once the algorithm terminates, the parameter values corresponding to the best point in the simplex represent the solution that minimizes the error using residuals.

Least square algorithm

The least squares algorithm is a method used to minimize the error between observed data points and a mathematical model. It achieves this by finding the best-fitting line (or curve) that minimizes the sum of squared residuals.

Residuals are the differences between the observed data points and the corresponding values predicted by the model. The algorithm calculates these residuals and aims to minimize their sum of squares, hence the name “least squares.”

In the case of a simple linear regression (fitting a straight line to data), the algorithm minimizes the sum of squared residuals by adjusting the slope and intercept of the line. The slope represents the relationship between the independent variable (x) and the dependent variable (y), determining how much y changes for a unit change in x.

The algorithm starts with an initial guess for the slope and iteratively adjusts it to reduce the sum of squared residuals. It does this by taking the derivative of the sum of squared residuals with respect to the slope and setting it to zero. Solving this equation gives the slope that minimizes the sum of squared residuals.

By minimizing the sum of squared residuals, the least squares algorithm finds the best-fitting line that represents the overall trend of the data and provides a measure of how well the model fits the observed data points. This method is widely used in various fields, including statistics, economics, engineering, and data analysis.

L-BFGS

L-BFGS (Limited-memory Broyden-Fletcher-Goldfarb-Shanno) is an optimization algorithm used for unconstrained optimization problems. It is particularly efficient for problems with a large number of variables.

The algorithm approximates the inverse Hessian matrix, which represents the curvature of the objective function, using a limited amount of memory. It builds and updates an approximation of the Hessian matrix based on the gradients of the objective function at different points during the optimization process.

At each iteration, L-BFGS combines the gradient information from the current iteration with the stored information from previous iterations to estimate the optimal step direction. It uses a line search technique to determine the step size that minimizes the objective function along that direction.

By iteratively updating the parameter values based on these steps, L-BFGS aims to converge to a local minimum of the objective function. The algorithm is efficient because it avoids explicitly computing and storing the full Hessian matrix, which can be computationally expensive for large problems.

In summary, L-BFGS is an optimization algorithm that uses limited memory to approximate the inverse Hessian matrix and iteratively updates the parameter values based on estimated step directions to converge towards a local minimum of the objective function.

1. Global optimisation

Markov Chain Monte Carlo

If we can't integrate something, approximate it by sampling.

MCMC is a sampler : it is based on likeliness and acceptance ratio. At the end of the process a posterior distribution or a chain of the parameters are obtained. We cannot say a particular theta, which is a parameter set is best fit.

We will need a function which returns a number corresponding to how good a fit your model is to the data for a given set of parameters.

Bayesian thinking is combining prior beliefs and current events. The posterior can be computed say the probability that there will be rice for lunch today.

One MCMC method is the Metropolis Hastings algorithm. It can be used to compute distribution over the parameters given a set of observations and a prior belief. For this method, we need a proposal distribution to randomly walk in the distribution space. So at each point a new step is taken which is based on some rules of acceptance. If the current distribution is accepted it moves closer to the true destination or it will take a step back.

The “emcee” package, which stands for “MCMC Hammer,” is a popular Python package used for performing Markov Chain Monte Carlo (MCMC) sampling. In the context of parameter estimation with the “lmfit” package, “emcee” is often used to explore the posterior distribution of the parameters.

Here’s a high-level overview of how the combination of “emcee” and “lmfit” works:

1. Model definition: First, you define your model function using the “lmfit” package. This model function represents the relationship between your input variables and the expected output.

2. Data and fit: Next, you provide your observed data to “lmfit” along with initial guesses for the model parameters. The “lmfit” package uses various optimization algorithms to find the best-fit parameter values that minimize the discrepancy between the model predictions and the observed data.

3. Parameter uncertainty estimation: Once you have obtained the best-fit parameter values, you can use “emcee” to explore the posterior distribution of the parameters and estimate their uncertainties. This step is particularly useful for understanding the range of plausible values for the parameters.

4. MCMC sampling: “emcee” employs an ensemble sampler called “affine-invariant ensemble sampler” to explore the parameter space efficiently. It generates multiple “walkers” that move through the parameter space, sampling from the posterior distribution. The walkers are iteratively updated based on a set of proposals, and the process continues for a specified number of iterations or until convergence criteria are met.

5. Posterior analysis: After the MCMC sampling is complete, you can analyze the resulting chain of parameter samples. This analysis may include computing statistics such as the mean and standard deviation of each parameter, examining the correlation between parameters, and visualizing the posterior distribution using histograms or scatter plots.

By using “emcee” in combination with “lmfit,” you can take advantage of the optimization capabilities of “lmfit” to find the best-fit parameter values and then utilize the MCMC sampling functionality of “emcee” to explore the full posterior distribution, providing a more comprehensive understanding of parameter uncertainties.

Useful links:

1. Markov Chain Monte Carlo (MCMC) methods

Simulated annealing Simulated annealing is a metaheuristic optimization algorithm that is inspired by the annealing process in metallurgy. It is commonly used to find approximate solutions to optimization problems, particularly in cases where the search space is large and the objective function is noisy or contains multiple local optima.

The basic idea behind simulated annealing is to mimic the process of annealing, where a material is heated and then slowly cooled to reduce its defects and reach a state of minimum energy. In the context of optimization, the “energy” corresponds to the objective function value that we want to minimize (or maximize).

Here’s a general overview of how simulated annealing works to optimize an error or objective function:

1. Initialization: Start with an initial solution or state. This can be a randomly generated solution or a known solution.

2. Perturbation: Make a small random change to the current solution to generate a new candidate solution. This change is typically referred to as a “move” or “neighborhood operation.”

3. Evaluation: Calculate the objective function value (error) for the candidate solution.

4. Acceptance or Rejection: Compare the objective function values of the current and candidate solutions. If the candidate solution is better (i.e., has a lower error for minimization problems), accept it as the new current solution. If the candidate solution is worse, accept it with a certain probability determined by a probabilistic acceptance criterion.

5. Cooling Schedule: Adjust a parameter called the “temperature” that controls the acceptance probability. The temperature is gradually decreased over time according to a cooling schedule. At higher temperatures, the algorithm is more likely to accept worse solutions, allowing exploration of the search space. As the temperature decreases, the algorithm becomes more selective, focusing on exploiting promising regions.

6. Termination: Repeat steps 2-5 for a predefined number of iterations or until a stopping criterion is met. This can be a maximum number of iterations, reaching a satisfactory solution, or running out of computational resources.

The key aspect of simulated annealing is the acceptance probability function, which determines the probability of accepting a worse solution. This probability is influenced by the current temperature and the magnitude of the difference in objective function values between the current and candidate solutions. As the temperature decreases, the acceptance probability decreases, favoring better solutions. However, the algorithm retains a certain level of randomness to avoid getting stuck in local optima.

By allowing occasional uphill moves (accepting worse solutions) early in the optimization process and gradually reducing the acceptance probability, simulated annealing can effectively explore the search space, escape local optima, and converge to a near-optimal solution.

It’s important to note that simulated annealing is a stochastic algorithm, meaning that it involves randomness. Therefore, the quality of the solution obtained can vary across different runs of the algorithm.

Particle Swarm Optimization

Particle Swarm Optimization (PSO) is an optimization algorithm inspired by the social behavior of bird flocking or fish schooling. It is commonly used to solve optimization problems where a fitness function needs to be minimized or maximized.

In PSO, a population of candidate solutions, referred to as particles, moves through the search space to find the optimal solution. Each particle represents a potential solution and is associated with a position and velocity vector. The position vector corresponds to a potential solution in the search space, and the velocity vector determines how the particle moves through the search space.

The movement of particles in PSO is influenced by their own best-known position, called personal best, and the best-known position of the entire population, called global best. These positions are updated during the optimization process based on the fitness function evaluation.

To measure the error in PSO, the fitness function is used. The fitness function quantifies the quality of a candidate solution and assigns a fitness value based on how well the solution satisfies the optimization criteria. The goal is to minimize the fitness function, which corresponds to minimizing the error or maximizing the performance of the system being optimized.

The error in PSO is typically calculated as the difference between the actual value or performance of the system and the target value or desired performance. For example, if the fitness function represents a regression problem, the error can be defined as the difference between the predicted values and the actual values of the training data.

The particles in PSO adjust their positions and velocities based on the error or fitness value. By updating their positions and velocities, particles explore the search space to find the optimal solution. The personal best and global best positions are also updated based on the error, allowing the particles to converge towards the optimal solution over iterations.

The PSO algorithm continues to update the positions and velocities of particles until a stopping criterion is met, such as reaching a maximum number of iterations or achieving a desired level of error. At the end of the optimization process, the particle with the best-known position represents the optimal solution found by the algorithm.

Overall, the error in PSO is used as a guiding metric to direct the movement and exploration of particles in the search space, enabling them to find the optimal solution for the given optimization problem.

Genetic algorithm

Genetic algorithm (GA) optimization is a search algorithm inspired by the process of natural selection and evolution. It is commonly used to solve optimization problems where traditional methods may be inefficient or infeasible. In GA, a population of candidate solutions evolves over multiple generations to find an optimal or near-optimal solution.

In the context of GA, the term “error” is often associated with the fitness function, which evaluates the quality or suitability of each candidate solution. The fitness function represents the problem’s objective or evaluation criteria, and it assigns a numerical value, often called a fitness value, to each candidate solution.

The optimization process in GA involves iteratively improving the solutions in the population over generations. At each generation, the individuals with higher fitness values are more likely to be selected for reproduction, while those with lower fitness values have a lower chance of being chosen as parents. This selection process is often referred to as “fitness proportionate selection” or “roulette wheel selection.”

After selection, the chosen individuals undergo genetic operators, primarily crossover and mutation, to produce offspring. Crossover involves combining genetic information from two or more parent individuals to create new solutions. Mutation introduces small random changes in the genetic information of individual solutions to explore new regions of the search space. These genetic operators aim to mimic the natural genetic variation and inheritance process.

The offspring generated through genetic operators form the next generation, replacing the least fit individuals from the previous generation. The process of selection, crossover, and mutation is repeated for several generations, allowing the population to evolve and converge toward better solutions.

The error in GA optimization is typically related to the fitness values of the candidate solutions. In most cases, the objective is to minimize the error or maximize the fitness value. The error could represent the discrepancy between a candidate solution’s performance and the desired or optimal outcome. For example, in a problem of optimizing a mathematical function, the error may be the difference between the function’s output and the target value.

The GA optimization process aims to reduce this error or minimize the objective function by iteratively refining the population of candidate solutions. As the generations progress, the average fitness value of the population tends to improve, and the error decreases. Eventually, after multiple iterations, the algorithm may converge to a satisfactory solution or reach a termination condition, such as a maximum number of generations or a predefined error threshold.

Overall, the error in genetic algorithm optimization refers to the measure of the discrepancy between a candidate solution’s performance and the desired outcome, which the algorithm attempts to minimize through the evolutionary process.

Gaussian Process Regression

Gaussian Process Regression (GPR) is a probabilistic machine learning technique used for regression tasks. It is based on Gaussian processes, which are a collection of random variables, any finite number of which have a joint Gaussian distribution.

In GPR, instead of assuming a specific functional form for the relationship between input variables (features) and output variables (target), it models the underlying function as a Gaussian process. A Gaussian process is fully defined by its mean function and covariance function (also known as kernel function).

The mean function represents the expected value of the target variable given the input variables, while the covariance function captures the relationships and similarities between different input-output pairs. The choice of the covariance function determines the smoothness, stationarity, and other properties of the modeled function.

During the training phase, GPR estimates the parameters of the mean and covariance functions from the provided training data. The model uses Bayesian inference to compute a posterior distribution over the possible functions that could explain the data. This posterior distribution is then used to make predictions for new, unseen data points.

GPR provides several advantages, including:

Flexibility: Since GPR does not assume a specific functional form, it can model complex relationships between variables without imposing strong assumptions.

Uncertainty estimation: GPR provides a measure of uncertainty for each prediction. This is particularly useful in cases where reliable uncertainty estimates are important, such as in decision-making under uncertainty or when dealing with noisy or sparse data.

Interpolation and extrapolation: GPR can effectively interpolate between observed data points and make predictions at unobserved locations, even in regions with limited or no data.

Bayesian framework: GPR naturally incorporates prior knowledge and allows updating the model as new data becomes available.

However, GPR can be computationally intensive for large datasets, as its time and space complexity scales cubically with the number of training examples. Various approximation techniques and sparse methods have been developed to address this limitation.